hypergeometric distribution for proximal gene enrichment

Question

[tonja.r]

I was reading a paper (GREAT improves functional interpretation of cis-regulatory regions) and they refer that hypergeometric distribution is used for assessing the proximal gene enrichment in ChIP-seq data.

In a typical analysis, one compares the total fraction of genes annotated for a given ontology term with the fraction of annotated genes picked by proximal binding events to obtain a gene-based P value for enrichment. (a) This procedure has a fundamental drawback: associating only proximal binding events (for example, under 2-5 kb from the transcription start site) typically discards over half of the observed binding events (a).

They propose that one could extend the regulatory domain and use a binomial test for distal binding sites. Is it possible to extend the regulatory domain (the way they do it in the paper) and apply a hypergeometric test on those domains?

[LauferVA]

Hi Tonja, I am sorry, but the sentence, "Somehow I do understand why it is not possible to extend the regulatory domain (the way they do it in the paper) and apply a hypergeometric test on those domain?" is unclear. Do you mean you do not?

[tonja.r]

I corrected it

Answer 1

[LauferVA]

Hi Tonja,

The rationale for the use of a binomial test is described in the paper: http://www.ncbi.nlm.nih.gov/pubmed/20436461

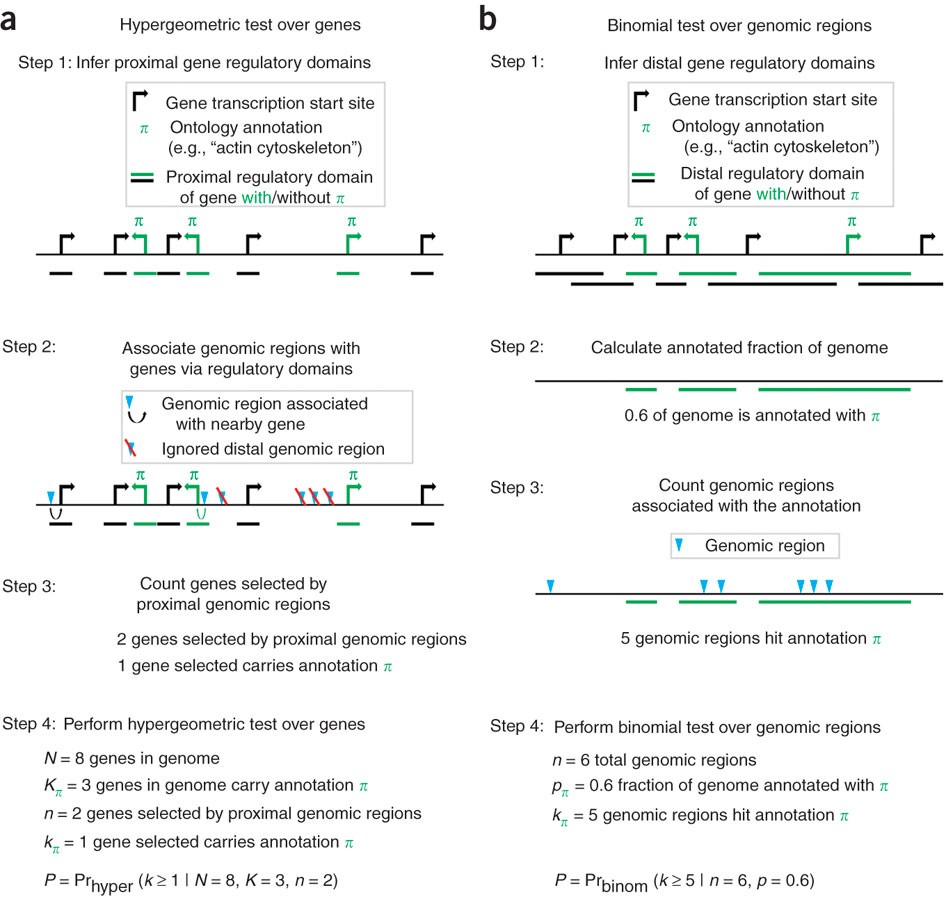
In the introduction, in the second paragraph, they say "...the standard approach to capturing distal events--associating each binding site with the one or two nearest genes, introduces a strong bias toward genes that are flanked by large intergenic regions' and then they further explain that this bias leads to the generation of false positive enrichment scores.

The hypergeometric test is not biased in this way for PROXIMAL regions because they do not have such wide variation in size (the authors state they are between 2-5kb). But the same cannot be said for DISTAL regions - they have huge variation in size.

So, to avoid this enrichment, the hypergeometric test is not used...Think of it this way, if you used the same procedure in Figure 1a as you did in Figure 1b (i.e., hypergeometric test both times), then genes that had huge flanking regions would pop up in your analysis way more than genes with shorter flanking regions, due to probabilistic considerations introduced by the sheer size of the region.

So, instead they define a regulatory domain and the number of bases that that covers (step 2 in Figure 1b), then convert to a fraction (see Results, page 495-496). This is a much better approach than using the hypergeometric test because it is free from the type of bias they describe.

In answer to your question, yes, you can use a hypergeometric test any time you wish to test for enrichment of items. However, in this case, applying it is likely to lead to a biased (systematically inaccurately estimated) test statistic.

If you still have questions after reading this, reading the paper plus references 12,15, and 16 should clarify the issue beyond and doubt.

[tonja.r]

Amazing answer! Thank you a lot. (However, I could find the answer to my question just by reading the paper more precise)

[LauferVA]

You're welcome. I hope it helped - let me know if there are some lingering doubts.

[tonja.r]

I looked at the paper again and found another question:

Enrichments under the binomial test may arise from clusters of noncoding regions all near one or a few genes with a particular ontology annotation, as well as from noncoding regions associating with many genes that possess a particular ontology annotation.

I can imagine the first case, when one have one gene and a cluster of genomic regions, it can happen that the regulatory domain is small, so that in results in the small p (small fraction of annotated genome). In fact, taking great amount of genomic regions, one gets a significant p-value.

But I have difficulties with imagining the situation "from noncoding regions associating with many genes that possess a particular ontology annotation."