I think there's some misconceptions operating here from the original questioner. First and foremost, a t-test is not just a way of calculating p-values, it is a statistical test to determine whether two populations have varying means. The p-value that results from the test is a useful indicator for whether or not to support your null hypothesis (that the two populations have the same mean), but is not the purpose of the test.
In order to carry out a t-test between two populations, you need to know two things about those populations: 1) the mean of the observations and 2) the variance about that mean. The single value you have for each population could be a proxy for the mean (although it is a particularly bad one - see below), but there is no way that you can know the variance from only one observation. This is why replicates are required for microarray analysis, not a nice optional extra.
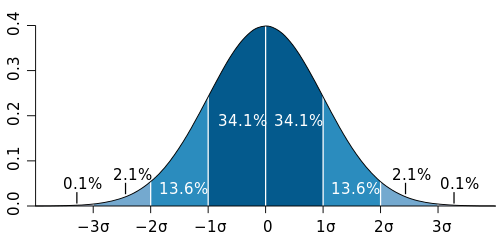
The reason a single observation on a single microarray is a bad proxy for the population mean is because you have no way of knowing whether the individual tested is typical for the population concerned. Assuming the expression of a given gene is normally distributed among your population (and this is an assumption that you have to make in order for the t-test to be a valid test anyway), your single individual could come from anywhere on the bell curve. Yes, it is most likely that the observation is somewhere near the mean (by definition, ~68% within 1 standard deviation, see the graph), but there is a significant chance that it could have come from either extreme.
Finally, I've read what you suggest about the hypergeometric test in relation to RNA-Seq data recently, but again the use of this test is based on a flawed assumption (that the variance of a gene between the 2 populations is equivalent to the population variance). Picking a random statistical test out of the bag, just because it is able to give you a p-value in your particular circumstance is almost universally bad practise. You need to be able to justify it in light of the assumptions you are making in order to apply the test.
BTW, your data does not look like it is in log2 scale (if it is, there's an ~32-fold difference between the renal and heart observations for the first gene above) - how have you got the data into R & normalised it?



Nag your supervisor to provide some more arrays and allow you to run the experiment again. The arguments to convince him or her are possibly that:
+1 because I can't give +2 or more.